Chris Tiee
 Researcher working with Michael Holst at CCoM
Researcher working with Michael Holst at CCoM
Donut Meister
Email: ctiee@ccom.ucsd.edu
Office: AP&M 5121
Research
My research interests lie at the intersection of analysis, geometry, partial differential equations, and their computational aspects. Lately, I have been looking at the finite element exterior calculus (FEEC), working with Hilbert complexes in general, and the general nature of boundary value problems. I successfully defended my PhD on 6/4/2015; the thesis is available here, with supplemental files here. An extended version of my PhD thesis with supplementary notes is available here. Or buy the bound version at Lulu.com. 
Recent Talks
PhD Defense: Applications of Finite Element Exterior Calculus to Evolution Problems
My PhD defense, given 6/4/2015.
Finite Element Exterior Calculus for Evolution Equations in Hilbert Complexes
Given at the CCoM Seminar, 2/10/2015
Also download the version with movies.
Finite Element Exterior Calculus for Geometric Problems
Given at the CCoM Seminar, 3/11/2014
Also download the version with movies (it'll download separately as a zip file rather than show up in your browser, though; they'll also only play in Adobe Reader).
Teaching
Spring 2016
Math 10C
Winter 2016
Math 170A
Fall 2015
Math 10B, Lecture B
Math 20D, Lecture D
Publications
M. Holst and C. Tiee, Finite Element Exterior Calculus for Parabolic Evolution Problems on Riemannian Hypersurfaces. Submitted for publication.
Available as arXiv:math.NA/1509.05524
Notes
Notes on Tensor Analysis
Notes attempting to demystify some of the vagaries of tensor analysis. Many issues raised in that document have since been resolved; updates forthcoming. In the meantime, a more concise version of this is included in Chapter 1 of the extended version of my thesis.
Match this 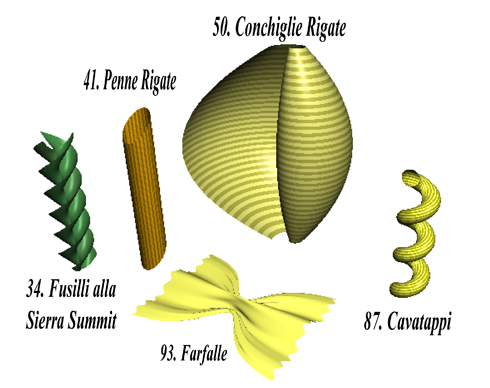 Pasta to these
Pasta to these
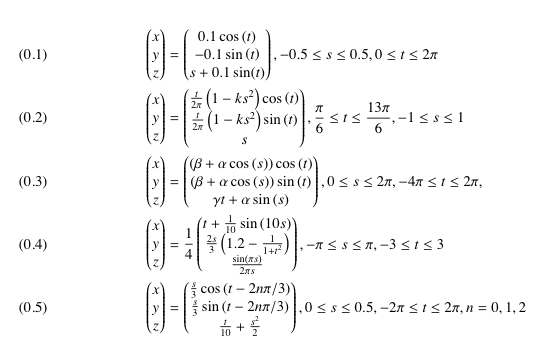 Parametrizations. (Answer key here)
Parametrizations. (Answer key here)
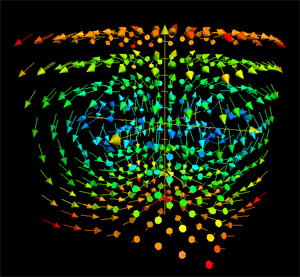
Why gradient vector fields have no curl
This phenomenon occurs in more general versions quite routinely in my research. Also, the proof that your parents lied to you when they said when they were your age, they had to walk to school uphill both ways.
Links
Center for Computational Mathematics (CCoM)
 My visualization blog, Nested Tori
My visualization blog, Nested Tori
 Pasta to these
Pasta to these
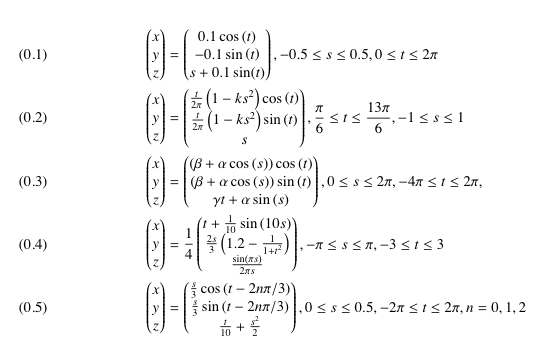 Parametrizations. (Answer key here)
Parametrizations. (Answer key here) Researcher working with Michael Holst at CCoM
Researcher working with Michael Holst at CCoM
 Pasta to these
Pasta to these
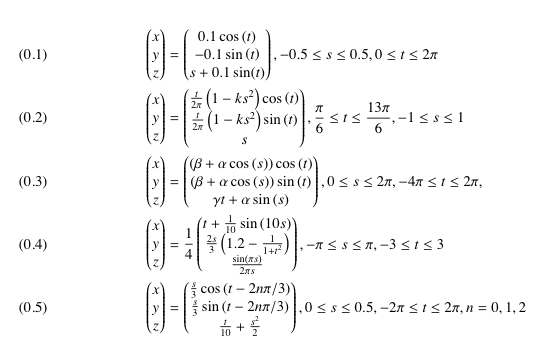 Parametrizations. (Answer key here)
Parametrizations. (Answer key here) My visualization blog, Nested Tori
My visualization blog, Nested Tori