
| Homework | Exam Info and Seating | Practice Exam, Midterm 1 | Practice Exam, Midterm 2 | Final Exam Info |
There is also TED for this course, though it will mostly be a place to check your grades. Piazza will still be the main place for discussion.
The course syllabus, containing most of this information, more official policies, and an approximate lecture schedule, is available in PDF form here.
MATLAB assignments are a required part of this course; it is somewhat independently administered; the schedule and assigments are up on the MATLAB for Math 20D page. Separate written homework will be assigned, but none yet, until I get it all straightened out with TED.
Office hours:
Thursdays 4p-6p
Fridays 11:30a-1:30p
| Section | Time | TA |
| D01 | Tu 4:00p-4:50p | Ashley Chen |
| D02 | Tu 5:00p-5:50p | Ashley Chen |
| D03 | Tu 6:00p-6:50p | Kuangyi Yang |
| D04 | Tu 7:00p-7:50p | Kuangyi Yang |
| D05 | Tu 8:00p-8:50p | Kuangyi Yang |
| D06 | Tu 9:00p-9:50p | Kuangyi Yang |
Section 1.1: 15-20, 22
Section 1.2: 1(a), 7, 12, 15
Section 1.3: 7, 12, 18, 20
Section 2.1: 1, 14, 15, 16, 19
Homework 2: due Wed, Oct 14 at the end of class
Section 2.1: 21,31
Section 2.2: 1, 2, 9, 15, 23, 30(a-e)
Section 2.3: 2, 10, 16
Section 2.5: 3, 6, 7
Homework 3: due Friday, Oct 23 at the end of class (note the change from Wednesday!)
Section 2.6: 1, 8, 10, 13, 15
Interesting OPTIONAL problem that relates integrating factors to Sec 2.1: 23
Section 3.1: 1, 5, 10, 18
Section 3.2: 3, 5, 7, 9
Section 3.3: 1, 3, 9, 11, 18, 20
Section 3.4: 1, 2, 6, 12
Homework 4: due Fri, Oct 30 at the end of class
Section 3.4: 23, 25, 28, 31
Section 3.6: 1, 2, 3 (ignore the instruction "check your answer using undetermined coefficients"), 5 (use integral sec(t) dt = ln|sec t+ tan t|), 7, 12 (leave it in integral form), 13 (remember to divide through to get y" by itself).
(hopefully, you'll find this shorter)
Homework 5: due Fri, Nov 6 at the end of class
Section 3.7: 26(a) (use general solution with sin and cos as in Section 3.4; and solve for c1 and c2 using the initial conditions, and abbreviate the imaginary part as mu). OPTIONAL, but good practice because I think it'll help develop your feel of DiffEq: 26 (b) and (c) also.
Section 7.1: 5, 6
Section 7.2: 1, 2, 11, 21, 22, 23
Section 7.3: 14
Note: Problem 15 (in an earlier edition of this assignment) has been removed. I thought it was a straightforward Wronskian question, but it is definitely a linear algebra subtlety which is beyond the scope of this class.
Homework 6: due Fri, Nov 13 at the end of class
Section 7.4: 4. OPTIONAL, for a more solid theoretical understanding of the Wronskian: 2, 3.
Section 7.5: 2, 3, 8, 15 [You can use Matlab Project 4 to help you graph these.]
Section 7.6: 2, 3 [You can use Matlab Project 4 to help you graph these.]
Homework 7: Due Fri, Nov 20, at the end of class (we have a midterm that day. I'll put a reminder on the board then). Note also that we're skipping Section 7.7.
Section 7.3: 16, 17, 18, 21 (there's a i sqrt(11) ... do not be alarmed).
Section 7.6: (Some of these were also on the last homework; this time, express the general real solution, i.e. including sines and cosines): 2, 3, 6, 9
Section 7.8: 1, 3, 4, 7
Note that MATLAB Project 4 has been postponed to be due on Monday. You can either use MATLAB project 4 to help you out with the graphing, or simply write in a verbal description of what kind of graph it will be, with certain key terms such as source, sink, node, saddle, and spiral.
Homework 8: Due Wednesday, December 2:
Section 5.1: 3, 5, 7, 9, 13, 17
Section 5.2: 1, 3, 5, 9, 11
Last Homework (no due date: you do NOT have to turn in):
Section 6.1: 1, 7, 9, 11, 15 (this topic may be on the final, so practice!)
The rest of this will not be on final but is sort of the logical conclusion and the rhyme and reason for the method of Laplace transforms, for your reference and future classes):
Section 6.2: 1, 3, 5, 11, 13, 39 (use the method of 39 without proof to do partial fractions)
Section 6.4: 1, 3, 5
Assigned Seating for Exams
Seats will be assigned for the exams. Each chair in the lecture hall has a small metal label on the part where you rest your back on:

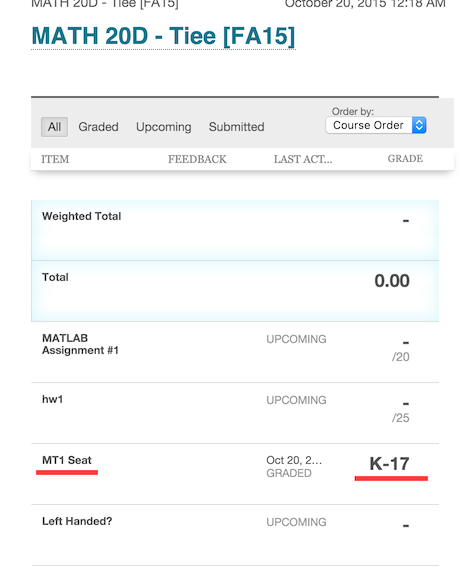
If you prefer a left-handed seat, please contact me about it as soon as possible, and we will change your assignment. To look up your seat assignment, check your grades on TED. There will be an "assignment" labeled "MT1 Seat", and your "grade" is your seat number (see screenshot; it's been underlined):
These are actual exams that were given in previous quarters, so they've actually been field-tested by real humans.
20D Midterm 1, Fall 2006. This test includes some reference information with the various types of differential equations. This would be a good idea to include on your note sheet. *hint hint*
20D Midterm 1, Winter 2013. (You will only be expected to know the difference between stable and unstable equilibrium solutions, though semistable was covered in a homework problem).
Practice Midterm 2's
Here are two midterms that were, again, actual exams from previous quarters, which most closely match what we've covered. There are many other practice exams out there from old quarters; you may, by all means, obtain them and use them as practice--but just be aware that there may be some stuff on them that we haven't covered, or, stuff that already has been covered on our first midterm. These ones given here have simply passed my own inspection.
20D Midterm 2, Fall 06 (here are solutions for it). Some comments: Problem 1 actually was mostly covered on the first midterm; the real new material is the Variation of Parameters. Like that professor, I will tell you the necessary integrals if they involve anything like trig sub or (God forbid) partial fractions. Skip 4c; we did not do that in class.
20D Midterm 2, Spring 15 (I'll post solutions soon). For problem 3, instead of using undetermined coefficients, use variation of parameters. This is a considerably easier exam than the previous practice, and ours will be closer to this one (but there will likely be a separate "reduction of order" problem).
Our Midterm 2 will be 4 questions long (instead of the 5 of the last midterm).
The final will be on Tuesday, December 8, from 3:00 PM to 6:00 PM, at Ledden Auditorium (same place as lecture). The same policies regarding electronic devices and calculators applies as in the midterms. Bring your IDs, a blue book, and two double-sided 8.5 x 11 inch pages of notes. My advice is to not re-use your note sheets from your midterms, but rather to make new ones from scratch. This is the best exam preparation ever; don't skip it! Seating will be assigned; check TED just as you did for the midterms and let me know if you need a left-handed seat.
The final will consist of 8 questions; 3 will be similar to Midterm 1 questions, 3 will be similar to Midterm 2 questions, and 2 on new material: a series question and a Laplace transform. I will post exam topics to Piazza. This means, it will be useful to get both of your midterms back from me and review them and the right answers (they will be great practice for 3/4 of your final!).
In addition, there is a Review Session this Saturday, December 6 in AP&M B402A (Calc Lab) at 1:00 PM - 3:00 PM as well as 4:00 PM - 6:00 PM. Both of them will be going over the same material; since seating is limited in that room, do not go to both. I will use an overflow room if it is necessary.