Math 170A, Winter 2016
Finals Week
-
(3/22/16) Your grades have been posted to TED and submitted. Here is the distribution of grades:
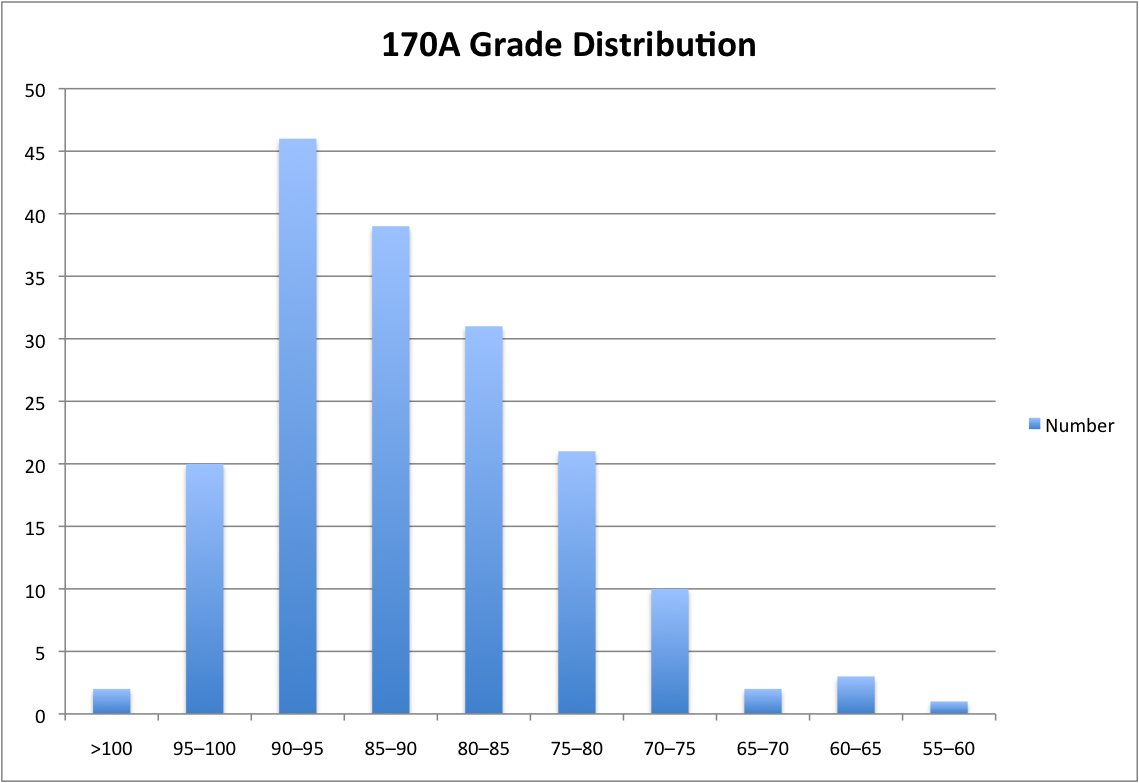
The stats were:
Mean: 85.8%
Median: 86.8%
Std Dev: 9.58% - (3/17/16) Ignore the request to check if your exams have been scanned in; you will not be able to see it, or the fact that it is, until they've been graded.
-
(3/17/16) The finals have all been scanned into Gradescope and the grading has begun.
Please log into Gradescope to make sure the exam is there and all 13 pages are present. Let us know immediately if anything is missing. - (3/16/16) Good luck on the final!
- (3/15/16) Seats have been assigned for the final exam. Due to technical delays, I only got the seating up just tonight. I sent a reminder via TED already, but doesn't hurt to send update here too (especially if you check a non-UCSD email more regularly). The procedure is exactly the same as it was for the midterms: log into TED and check the "grade" called "Final Seat" (your previous seats for Midterms 1 & 2 have been hidden, so you won't confuse it)
- (3/14/16) Happy Pi Day!!
- (3/12/16) We actually reached 80% CAPE participation, the highest in all of the math department. I'm surprised; I thought that all math profs did that trick. As promised, your lowest homework score will be dropped. In addition, Homework 5 is not going to be graded (but if you haven't done it, I suggest you do so anyway, because there will be a final exam problem just like it, except, of course, the arithmetic will be made easier since you won't have MATLAB to do it for you!)
Weeks 8-10
- (3/10/16) Additional review sessions on Saturday, March 12 from 2pm-4pm and Monday, March 14 from 5pm-7pm in AP&M B402A (Calc Lab) have been scheduled. Capacity is limited to 50, so if you can make the one in the usual room on Sunday (see update just before this one), please go there.
You will need your student ID to get into the building on Saturday (see post @228 on Piazza).
- (3/9/16) We will be having a review session on Sunday, March 13 from 3pm-5pm in PCYNH 106 (the usual room). I will post a poll on Piazza to get a headcount to see who can make it, and schedule another if necessary.
- (3/8/16) We are at nearly 57% for CAPE evaluations! (You have about a week left to submit yours!)
- (3/3/16) We are at nearly 40% for CAPE evaluations! (You have about 1.5 more weeks to submit yours!) Remember, Homework Drop occurs when we reach 75%.
- (3/2/16) Homework 5 is posted.
- (2/29/16) Midterm 2 is graded. Check your grades on Gradescope. The statistics:
Mean: 39.79 out of 55 (72.35%) Median: 42 out of 55 (76.36%) Stdev: 10.82
See the midterm solutions on Piazza. Just a word of warning for the final: $(A^T A)^{-1}$ cannot be generally expanded $A^{-1} A^{-T}$ unless $A$ is square!
- (2/26/16) Midterm: Same rules as last time, seating, etc.
- (2/23/16) Homework 4 is posted. Prioritize Section 8.4 for studying for the midterm; do the 8.3 and 8.7 homework afterward.
- (2/23/16) Seating assignments for Midterm 2 are on TED. Again, if you are left-handed, let me know (for anyone who contacted me for the first test, I saved your preference; you don't have to ask again.) Also, let me know if you do not see your seat assignment.
Weeks 6-7
- (2/14/16) Here's something to help you understand where we are going with iterative methods. A Painless Introduction to the Conjugate Gradient Method, which pretty much talks about Section 8.4 in the book to greater depth with more examples (it also recaps the Jacobi method). Note that they use some differing conventions (e.g. $x_{(k)}$ for our $x^{(k)}$), and they preview eigenstuff (referred to as "eigenthingies" and "eigendoohickeys").
- (2/11/16) Homework 3.5 is posted! It is a short assignment on intro to iterative methods. It is in fact about half as long as our regular assignments have been, as its name implies. It will be due at 11:59 PM Friday Feb 19.
This homework will count for one whole homework assignment. Additionally, if at least 75% of the class does CAPE reviews, your lowest homework assignment will be dropped. So please do those reviews when they come around (8th week). (Getting feedback is important, so the more people who do it, the merrier; I will not be able to read them until after the quarter ends; I can only see the level of participation).
- (2/6/16) The Lecture schedule has been updated. The main change is that we will be doing iterative methods earlier than planned, in place of eigenvectors and eigenvalues, which we will finish the quarter with. Iterative methods are a cornerstone of modern matrix computations, so getting to it earlier in the quarter should keep things interesting and prevent it getting lost in the Finals Week rush.
Weeks 4-5
- (2/4/16) Homework 3 is up. You can write it out like you'd do with any normal written homework (you do not have to take separate pictures of different problems, but it may help); Just remember to select the pages, which may be more than one, for each problem, by clicking the menu button in the lower right corner of the window, and choosing "Reselect Pages".
- (2/3/16) Read up on some summary information about what we've covered so far here. This should hopefully make all the multiplicity of options for matrix decompositions less bewildering. Consider it a "mid-quarter review."
- (2/1/16) Midterm 1 is graded. Its solution is posted on Piazza. Here are the stats (more details viewable on Gradescope):
- Mean: 35.88/50 (71.76%)
- Median: 39/50 (78%)
- (1/27/16)
Seating assignments are up. Here are the instructions:
Log into TED, and check your grades. You will see an "assignment" called MT1 Seat. That gives your seat number which should look like
A-35
(or, basically, Letter-numbernumber). This is your seat number for the Midterm.
If you are left-handed, let me know right away: I will change your assignment (and in fact, I've deliberately left the left-handed seats unassigned), and someone else who does not have a seat yet can take that vacated seat (the class is very full!)
Some of you may not have seat numbers yet: Do Not Panic. Aside from the response from left-handers, I am consulting with the Front Desk.
- (1/26/16) Homework 2 due date has been changed to Monday, February 1, at 11:59PM. This is to help people have one less thing to worry about (e.g. dealing with Gradescope wrinkles) before the midterm.
- (1/25/16) Extra Office Hours: I will be extending my office hours to 1-3PM Tuesday and Thursday this week for the midterm. Of course, you still can make an appointment if you can't make those times.
- (1/24/16) If you had trouble with submitting things on Gradescope for Homework 1, please send me the pictures of what you want to resubmit. (Gradescope won't allow students to do resubmissions after the due date, nor modify things in the regrade process, but will allow the instructor to do it for them). There will (still) be no penalty.
- (1/22/16) Friday's lecture on Least Squares includes both section 3.1 and 3.5 material (in particular, the sections called "Discrete Least Squares problem"). This means Homework 3.5.23 is actually easily doable (via the Normal Equations). The relevant theorem for that is 3.5.21, and the general discussion on page 241. We will cover the QR decomposition next week (Sections 3.2-3.3) next week.
- (1/21/16) Homework 1 has been graded.
For those of you who had trouble submitting the homework the first time around, you can resubmit it as a regrade request.UPDATE: see announcements 1/24/16. There will be no penalty.
Weeks 1-3
- (1/15/16) Homework 2 is posted; I also adjusted the schedule a little. Keep in mind that the approximate schedule is intentionally more ambitious (some might say, overly optimistic) than we will follow, again as a sort of insurance policy: if you over-prepare a little bit and we end up not getting to a certain topic, it's better than being very behind (very easy to happen in this quarter system!).
- (1/13/16) The problems from Homework 1 that were from Sections 1.6 and 1.7 have been moved to Homework 2. Only do the problems up through Section 1.5.
- (1/06/16) Here's some information regarding the MATLAB component of the course (it's below, but reproduced here for convenience):
Lab Information: As mentioned above, computer programming is an essential component of the course. That said, you are not expected to have a very advanced knowledge of programming and MATLAB techniques, nor do we claim that you will acquire such expertise in this course. MATLAB is available on AP&M lab computers (in B432 to be precise). It is also accessible via govirtual.ucsd.edu. See ACMS computing services (AP&M 1313) for details (or visit http://acms.ucsd.edu/students/govirtual/ and https://virtuallab.ucsd.edu/). Also, a number of open source (i.e., free) MATLAB alternatives are available, like GNU Octave. You simply need some programming environment to complete the assignments; it doesn't matter which.
Finally, see the MATLAB projects for Math 20F page for the projects and expected level of knowledge of MATLAB in case you didn't take, or it's been a while since you've taken, Math 20F. - (1/05/16) Homework 1 is posted. Just from yesterday's lecture, you can already do at least 1.1.8, 1.1.10, and 1.1.25. (and doing them will definitely clarify yesterday's lecture.) Also, the lecture schedule was revised a bit to be more nuanced, by section; some of the chapters will not be completely covered. But of course, check back frequently, because it'll be still subject to change.
- (1/04/16) Office hours will be: Tuesdays and Thursdays at 1:00p-2:00p (and also, of course, by appointment) in AP&M 5121
- (1/04/16) Hope you had a good first day of class. The first "dummy" assignment (really, the "zeroth" assignment) has been posted: it is mainly an exercise to get familiar with how to submit homework via gradescope. For those of you who have not already been added (for example, if you are an Extension student or on the wait lists), you can manually add yourself. Use the code 96KPKM.
- (1/02/16) Welcome! This is the initial setup of the webpage to get us started, for the benefit of anyone checking in early before the start of lectures. The first day of class is Monday, January 4, 2016. Not everything is up yet!
Office: AP&M 5121
Office hours: Tuesdays and Thursdays at 1:00p-2:00p, or by appointment.
Contact: ctiee@ccom.ucsd.edu
Printable version of this page (the syllabus): http://ccom.ucsd.edu/~ctiee/classes/170a/170a-syllabus-printable-version.pdf
Class Forum and Email Policy:
The best way to keep up-to-date about the course is via this course's Piazza page.
Sign up for this class on Piazza here. (Or look for an activation email from Piazza: data from TED was transferred over and you have been sent an invitation; check your official UCSD email address.) Piazza includes a discussion forum to ask general questions that can be answered by the instructor, TAs, or fellow students. To help accommodate people who may feel uncomfortable posting with their identities, anonymous postings are also allowed. Piazza also has an equation editor that allows display of math notation not available in email.
Because of these available resources, and the anticipated large size of the class, please check Piazza first (and maybe ask there), and then this webpage, before sending emails. Any such email answerable by other means will not get a response. Many questions about homework assignments will require in-depth responses, which are more appropriately answered in office hours; in that case, email should primarily be used to set up appointments in case you cannot make it to an office hour. Please be considerate and remember that I am a fellow human who has other life responsibilities outside of work, so not every email, especially those out of reasonable working hours, can be expected to receive a prompt response.
There is also TED for this course, though it will only be, for our purposes, a place to check your grades. Piazza will still be the main place for discussion.
Lecture Meeting Times and Location: MWF 12:00p-12:50p in Pepper Canyon Hall (PCYNH) 106
Sections and TAs: Discussion section is important for you to get practice with the homework and to get clarifications. The section times and locations are as follows:
| Section | Time | TA | Location |
| A01 | W 5:00p-5:50p | Francesca Grogan | AP&M 2301 |
| A02 | W 6:00p-6:50p | Yi Luo | AP&M 2301 |
| A03 | W 7:00p-7:50p | Jeremy Schmitt | AP&M 2301 |
| A04 | W 8:00p-8:50p | Jeremy Schmitt | AP&M 2301 |
| A05 | W 4:00p-4:50p | Francesca Grogan | AP&M B412 |
Catalog Description: 170A. INTRODUCTION TO NUMERICAL ANALYSIS: LINEAR ALGEBRA (4)
Analysis of numerical methods for linear algebraic systems and least squares problems. Orthogonalization methods. Ill-conditioned problems. Eigenvalue and singular value computations. Three lectures, one recitation. Knowledge of programming recommended.
Textbook: Fundamentals of Matrix Computations, Third Edition, by David S. Watkins.
Prerequisite: Math 20F (knowledge of programming basics or MATLAB basics, which should have been covered in 20F, is highly recommended [but see below in Lab Information and Grading and Exam policies])
Lab Information: As mentioned above, computer programming is an essential component of the course. That said, you are not expected to have a very advanced knowledge of programming and MATLAB techniques, nor do we claim that you will acquire such expertise in this course. MATLAB is available on AP&M lab computers (in B432 to be precise). It is also accessible via govirtual.ucsd.edu. See ACMS computing services (AP&M 1313) for details (or visit http://acms.ucsd.edu/students/govirtual/ and https://virtuallab.ucsd.edu/). Also, a number of open source (i.e., free) MATLAB alternatives are available, like GNU Octave. You simply need some programming environment to complete the assignments; it doesn't matter which.
There are two midterms (on Friday 1/29/16 and Friday 2/26/16) and a final exam (on Wednesday 3/16/16). The grading breakdown is as follows:
| Category | Weight |
| Homework | 30% |
| Midterm 1 | 15% |
| Midterm 2 | 15% |
| Final | 40% |
Here are the main points to remember about exams:
- You may bring an 8.5 x 11, double-sided sheet of notes to the midterms, and two such note sheets to the final.
- No make-up exams will be given. In the case of, and only in the case of, a medical emergency, with a doctor's note, you may be excused from an exam, and your grade will be determined by re-weighting the other exams.
- No calculators will be allowed (or needed) on the exams.
- Exams will be heavily based on homework. Therefore it is to your advantage to do the homeworks, go to lecture, discussion sections, and office hours to get proper feedback, even after you have submitted it or received a grade for it, and even if such a grade received is good.
- Grades will be adjusted ("curved") in a way so that an average grade will be no lower than a B-. However, we will strive to make exams in a fair manner that eliminates the need to adjust the grading scale: the curve exists as an insurance policy for differences in opinion of what I think is "reasonable" and "based on homework".
The homework will be from the textbook, and will include a number of exercises in MATLAB. No late homework will be accepted except for medical reasons. The electronic submission system won't count it if it is late, so due dates will deliberately be placed late at night.
| Assignment | Due Date | Description |
| Homework 0 | Friday 1/8 11:59PM | This is not a "real" assignment to get you all familiar with Gradescope and procedures: Turn in a pdf to gradescope.com containing your name and the message "Hello World!" |
| Homework 1 | Friday 1/15 11:59PM |
NOTE: For this and all following assignments, note that the book sprinkles the exercises throughout each chapter, rather than collects a bunch of exercises at the end of each chapter. This is to encourage active reading of the material. The exercises are numbered within each subsection, and they are numbered along with everything else: if there's an exercise after, say, Theorem 1.2.3, it will be called Exercise 1.2.4. Similarly, Exercise 1.1.8 follows Equation 1.1.7 (written (1.1.7) in the text). This, while seeming less logical, makes it easy to find an exercise: simply follow the numbering (regardless of what gets numbered) until you find the right one. Here are the exercises: 1.1.8 (copy/paste the output of the randn's and the matrix multiplication in that problem for your answer), 1.1.10 (use the code in 1.1.9 to get yourself started; the part (b) is simply replacing the line b=A*x), 1.1.25, 1.2.4, 1.3.4, 1.4.15, 1.4.16, 1.5.9. Note that 1.6.4, 1.7.10 will be moved to the next homework.. |
| Homework 2 | Monday 2/1 11:59PM | 1.6.4, 1.7.10, 3.1.5, 3.2.8, 3.2.14, 3.3.7, 3.3.10, 3.4.22, 3.5.23 . (Note that we are skipping Chapter 2 for now and then coming back to it, because Least Squares is just that important.). 3.5.23 is actually easily doable using the Normal Equations (covered in lecture on 1/22). The relevant theorem for that is 3.5.21, and the general discussion on page 241. |
| Homework 3 | Friday 2/12 11:59PM | 2.2.6, 4.1.6, 4.1.15, 4.2.8, 4.2.12, 4.3.8, 4.3.9 [Hint for the last one: Definitely use the condensed version. One column is very obviously a multiple of the other, therefore it is rank-deficient, the rank being only 1. This means the Σ will be a 1 × 1 matrix. Its value must compensate for all the normalization that goes on into making orthonormal basis vectors]. |
| Homework 3.5 | Friday 2/19 11:59PM | 8.1.9, 8.1.12, 8.2.4, 8.2.12, 8.2.24 I will probably do substantial portion of two of those in class, so go to class! |
| Homework 4 | Wednesday 3/2 11:59PM | 8.4.7a, 8.4.8a, 8.4.12, 8.4.22 (remember, $A$ is SPD, so eigenvalues are just its singular values and $U=V$ in its SVD), 8.3.14 (Suggestion: Prioritize 8.4 homework problems over 8.3 problems for midterm study. Use without proof $\rho(G)$ in Table 8.5 in the textbook, right between Exercises 8.3.12 and 8.3.13) Optional: Write an algorithm in Matlab implementing (8.3.15) and (8.7.1). |
| Homework 5 | Wednesday 3/9 11:59PM | 5.1.19 (I did some of this in lecture), 5.2.6, 5.2.17 (The relation of Eigenstuff and SVD), 5.3.6 (use the code from 5.3.10), 5.3.10 (your "lab assigment"). |
| Week | Topics Covered |
| Week 1 (1/4-1/8) |
1.1-1.5:
Brief review of background and notation,
Cholesky Factorization.
|
| Week 2 (1/11-1/15) |
1.4-1.6
More Cholesky factorization, block algorithms, and banded/sparse matrices.
Homework 1: 1.1.8, 1.1.10, 1.1.25, 1.2.4, 1.3.4, 1.4.15, 1.4.16, 1.5.9. |
| Week 3 (1/19-1/22) [Note: MLK Jr. Day is on 1/18, and there will be NO CLASS] |
1.7, 3.1-3.2:
LU Factorization, and Intro to Least Squares.
|
| Week 4 (1/25-1/29) |
3.3-3.5, More Least Squares, review, and Midterm:
Covering Chapters 1-3.
Homework 2: 1.6.4, 1.7.10, 3.1.5, 3.2.8, 3.2.14, 3.3.7, 3.3.10, 3.4.22. Midterm 1. Covers: 1.1-1.7, 3.1-3.4. |
| Week 5 (2/1-2/5) |
2.1, 4.1-4.2:
The Singular Value Decomposition (SVD)
|
| Week 6 (2/8-2/12) |
4.3, 8.1-2 The Moore-Penrose Pseudoinverse; Intro to Iterative Methods Homework 3. |
| Week 7 (2/16-2/19) [Note: Presidents' Day is on 2/15, and there will be NO CLASS] |
8.2-8.4: Iterative Methods. Homework 3.5. |
| Week 8 (2/22-2/26) |
Review and Midterm: Covering Chapters 4 and 8. Midterm 2. Covers: 4.1-4.3, 8.1-8.4 |
| Week 9 (2/29-3/4) |
Homework 4. 8.7, 5.1-5.2: Wrap-up of Iterative Methods, Eigenvalues and Eigenvectors. |
| Week 10 (3/7-3/11) |
Review for Final: Covering Main Parts of Chapters 1-5 and 8. Homework 5. |
| Final WED 3/16 11:30a-2:30p (Location TBA) |
Final Exam: Covers: Main Parts of Chapters 1-6 and 8. In particular: Covers Homeworks 1-5. Very specifically: Covers sections 1.1-1.7, 2.1, 3.1-3.5, 4.1-4.3, 5.1-5.3, 8.1-8.4, 8.7. Review Sessions: Saturday, March 12 from 2pm-4pm in AP&M B402A (calc lab) Sunday, March 13 from 3pm-5pm in PCYNH 106 (the usual room) Please try to attend this one if possible; the others have limited capacity. Also beware of Daylight Saving Time ("Spring Forward"), which removes Sunday's 2am. Monday, March 14 from 5pm-7pm in AP&M B402A (calc lab)
Extra Office Hours:
Francesca: Tuesday 3/15 10am-12pm
Chris: Tuesday 3/15 12pm-2pm
|