Weeks 9-Finals
"Evaluate the double integral $$\int \int_R (x^2+xy)\,dA$$, where $$R$$ is the square in the plane having vertices $0,0),(1,1)$, $(1,0)$, and ${\color{red}{(0,1)}}$" and "Evaluate the following integral in both orders: \[ \int_0^1 \int_{\color{red}0}^1 4 y \,{\color{red}{\sin(x)}}\,dx\,dy. \]" [the bottom limit has been replaced by $0$, and there is no square inside the $\sin$]. Solutions will be posted on Tuesday (and also, these alternate versions).
- Your lowest homework score will be dropped.
- The last day of lecture (and quite possibly the last two days) will be a review of the most important concepts (instead of trying to wedge in more multiple integrals)... and...
- The grading option that is "the best of two" will give only 50% of the weight to the final, not 60%.
Weeks 5-8
- Partial Derivative Basics (Sections 14.1-14.2). Basically, know how to compute partial derivatives: just the usual derivatives where you treat the other variable as a constant. In particular, much confusion in partial derivatives stems from not being able to see what is constant, and wondering why is zero sometimes and not zero at other times. To clarify, consider these two rules:
- $$\frac{\partial}{\partial x} (x+c) = 1$$ [the constant goes to zero and drops out, because it's added to $$x$$] but
- $$\frac{\partial}{\partial x} (cx) = c$$ [the constant stays around, because it's multiplying $$x$$].
- The Differential and Gradient (Sections 14.3-14.4). The differential
$$df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy$$
and gradient
$$\nabla f = \frac{\partial f }{\partial x} \vec{i} +\frac{\partial f }{\partial x} \vec{j}$$
both carry exactly the same information (namely, bundling the two partials together to form a new entity with superpowers), but are used in different contexts. The differential is for calculating small changes in $$z$$ given small changes in $$x$$ and $$y$$.
The gradient is used to:
- Find directional derivatives: partials in any direction you want, not just in $$\vec i$$ and $$\vec j$$. This is why it has superpowers: from just derivatives in two directions, it is enough to find them in all directions.
- Find the direction of the maximum rate of change, as well as the maximum rate of change itself: the max rate of change is the magnitude $$\|\nabla f\|$$, and the direction is the unit vector $$\nabla f/\|\nabla f\|$$.
- The Chain Rule. (Section 14.6) In particular, remember those diagrams: multiply along each pathway to the variable you want to find the partial with respect to, and add up the results of all the paths.
- Second Partial Derivatives (Section 14.7). Partials are so fun that we can do them over and over again. Remember that the mixed $$f_{xy}$$ is the same as $$f_{yx}$$. [Skip the thing about Taylor polynomials]
- Classification of Critical Points (Section 15.1). This is undoubtedly a trickier section, because some of those tests are hard to remember offhand. Make sure to write this on your cheat sheet:
- Critical point is where $$f_x = f_y = 0$$ or $$\nabla f = \vec 0$$.
- Take $$D = f_{xx}f_{yy} -f_{xy}^2$$ at each critical point, called the discriminant.
- If $$f_{xx} > 0$$ and $$D >0$$, it is a minimum
- If $$f_{xx} < 0$$ and $$D>0$$, it is a maximum
- If $$D < 0$$, it is a saddle point (and guaranteed to neither be min nor max).
- If $$D = 0$$, scream bloody murder; it could be anything. Barring a major boneheaded mistake on my part, I will not put an example with $$D=0$$ on the test.
- Optimization problems (Section 15.2). This is basically the word-problem and applications version of Section 15.1. Be able to translate whatever "cost" function into a formula. I will try to minimize nasty algebra with this one, and will give a better example on Monday.
The following topics will not be covered:
- Anything explicitly from Midterm 1. By explicit, I mean, there will be no question directly asking you "Find the dot product of ...". However, if you need to use the dot product (say, the directional derivative of something, $$\nabla f \cdot \vec u$$), that's fair game.
- Gradients and directional derivatives for functions of 3 or more variables (Section 14.5).
- The Physical Chemistry example in 14.6 (the relevant topic is partial derivatives with respect to whole different sets of variables).
- Taylor polynomials (part of Section 14.7)
- General theory of differentiability (Section 14.8)
- Any critical points for which $D=0$.
- Minimization/Maximization with constraints/Lagrange Multipliers (Section 15.3, even though we'll start talking about that on Monday and Wednesday).
| Mean | 19.90 (79.60%) |
| Median | 20 (80%) |
| Standard Deviation | 3.61 (14.44%) |
| Min | 8 (32%) |
| Max | 25 (100%) |
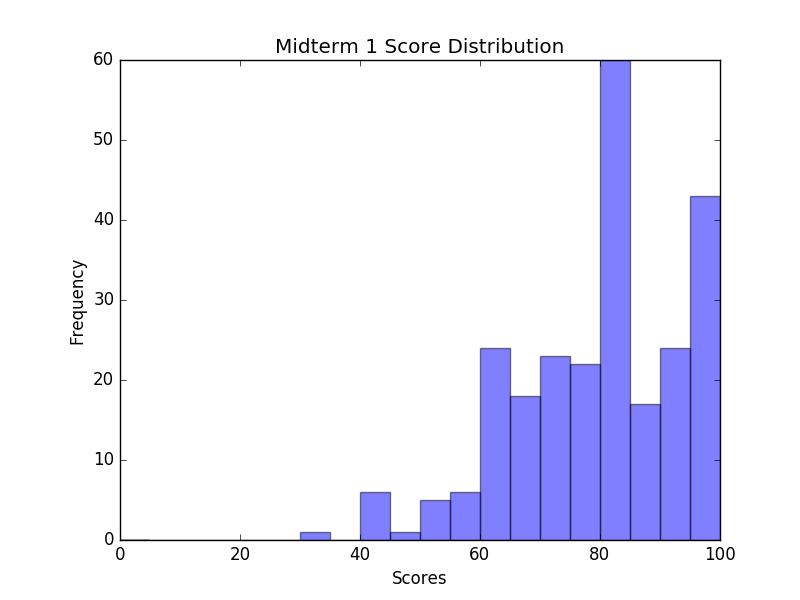
Weeks 1-4

The left-handed seats have been left unassigned, so if you are in fact left-handed, let me know (your preference, of course, will be recorded for next time).
Check the Center Hall seating chart to see in advance where to sit.
You must sit in your assigned seat (unless there is a problem, in which case, of course, we will reseat you) and we will check. We also reserve the right to reseat anyone as well.
Good luck; and remember I have office hours tomorrow at 12; come if you have last-minute questions.
- A blue book
- An 8.5" x 11" handwritten cheat sheet (double-sided). Don't photocopy; writing your cheat sheet is the best damn studying you will ever do; I guarantee it.
Other notes:
- No calculators are allowed (or needed)
- No other electronic devices--turn those phones off!
- Seats will be assigned. We will check. Look on TED the night before (or email me, if you are taking the course through Extension and cannot access TED). If you are left-handed, please let me know; it will affect your seat assignment.
Topics (Reading: Sections 12.1-12.4 and 13.1-13.3 and the first part of 13.4)
- Basic geometry of 3D space
- Basic graphs of functions z=f(x,y) [NO drawing, only matching!]
- Contour plots [NO drawing, only matching and/or finding their equations]
- Slicing (know what they are and contour plots as special case)
- Linear functions: how to recognize when something is linear.
- Vector basics, displacements
- Basic vector operations (addition, subtraction, and scalar multiplication)
- Magnitude and direction of vectors
- Resolving vectors into components
- Velocity vectors
- Dot products
- Very basics of cross products: their definition as directed area and the formula defining it.
These topics will NOT be covered:
- Actual drawing of any 3D graphs
- Actual drawing of contour plots
- Finding equations of surfaces for anything more complicated than planes
- Dealing with angles between vectors that are anything other than standard unit circle special angles from trig (ONLY: 30, 45, 60, 90, 120, 135, 150, or 180-degree angles can show up. HINT: write sines and cosines of this on your cheat sheet) [Without a calculator, you can't compute sines and cosines or find arc cosine of anything more complicated than this]
- More complex applications of cross products
- Anything from Chapter 14