| Michael Holst | ||
| https://ccom.ucsd.edu/~mholst/ |
Distinguished Professor of Mathematics and Physics UC San Diego |
|
|
 Applications of
FETK
in Biophysics
Applications of
FETK
in Biophysics
The finite element code FETK has been used successfully to build adaptive numerical approximations of solutions to the Poisson-Boltzmann equation, to generate the electrostatic field around a complex biomolecule. In the examples below, the dielectric discontinuity representing the solvent accessibility of the tRNA molecule is computed with Don Bashford and Tony You's SolvAccVol library. The discontinuities drive the error estimator in the adaptive bisection algorithm in FETK by causing abrupt changes in the gradient of the discrete solution. Below is an example; a 2D cartoon case appears here. The blue represents an isosurface of 0.8 kT/e, and the red represents an isosurface of -0.2 kT/e. The outer sphere is used to impose boundary conditions. 

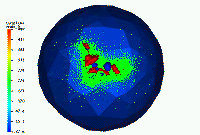



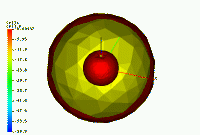


The isosurface pictures were made by FETK and GMV. The tRNA data and the SAV software is courtesy of Don Bashford. The space-filling pictures of tRNA were made using SG. The paper describing the use of FETK to solve the Poisson-Boltzmann equation adaptively can be found here. A second paper containing a sequence of numerical experiments using a very sophisticated Poisson-Boltzmann solver constructed on top of FETK, called APBS, can be found here. The paper describing the parallel computing approach employed in FETK, which is joint work with Randy Bank, can be found here. Here is the standard form of the nonlinear Poisson-Boltzmann equation: 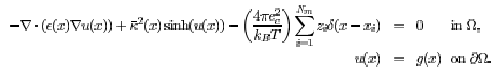
Here is some related stuff:
|
