[Home]   [  News]   [  Events]   [  People]   [  Research]   [  Education]   [Visitor Info]   [UCSD Only]   [Admin]
Home > Research > Topics
Search this site:


Directors:
Randolph E. Bank
Philip E. Gill
Michael Holst

Administrative Contact:
[ Click to Send Email ]

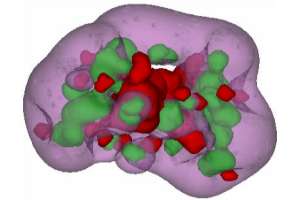
Research Areas

The UCSD CCoM faculty have research interests that span a wide range of mathematical and application areas, and have collaborative ties that transcend disciplinary boundaries. The research efforts are motivated by challenging, real-world applications in the physical and biological sciences, computer science, and engineering, while being grounded in rigorous mathematics. In particular, it covers the full spectrum of fundamental mathematical research, mathematical modeling and analysis, algorithm development, numerical implementation and software development.

Electrostatics Model
Electrostatics Model
Mathematical Areas
  • adaptive and multiresolution methods
  • applied, functional, and global analysis
  • computational geometry and mesh generation
  • discrete differential geometry
  • discrete models for classical and quantum systems
  • geometric mechanics and control
  • geometric numerical integrators
  • geometric, global, and nonlinear PDEs
  • interface problems, including level set methods
  • nonlinear and global approximation theory
  • numerical analysis, including error estimation
    (a priori and a posterori)
  • numerical linear algebra
  • numerical methods for PDEs, including finite element methods
  • numerical optimization, including linear, nonlinear, and semidefinite programming
  • parallel computing and domain decomposition
  • quantum computing
  • topological analysis of large data sets

Application Areas
  • Autonomous robots, underwater vehicles, and spacecrafts
  • Fluid and gas dynamics, including Navier-Stokes and Euler equations
  • General relativity
  • Image and signal processing
  • Magnetohydrodynamics (MHD)
  • Mathematical physics, chemistry, and biology
  • Nonlinear elasticity and solids