A Novel Paradigm for Parallel Mesh Generation
The problem we are solving is a standard convection-diffusion equation. The region is specified by a simple description of the boundary, called a skeleton . This skeleton is a facsimile of the UCSD logo. The convection is of strength 10^3 directed downward, resulting in some interesting boundary layers. We will solve this problem using a parallel adaptive mesh paradigm which allows the majority of the computation to be done in parallel with little communication.
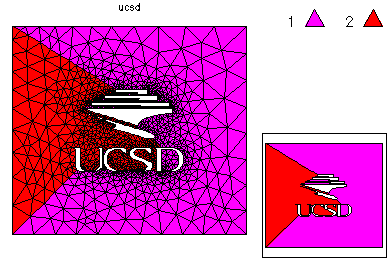
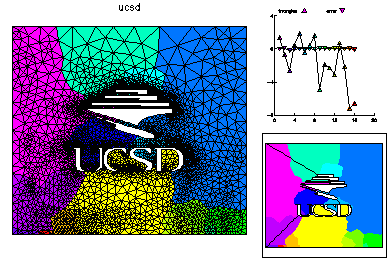
An initial mesh was created from the skeleton. This mesh was adaptively refined to form a mesh with 5000 vertices. This mesh is partitioned for 16 processors according to equal error, where the error is estimated via an a posterior error estimator. This is a small calculation and was done on only one processor. On the right the load balance is shown without element edges lined with black, and elements are colored according to size.
Here is the coarse grid solution. Each process is given the entire coarse problem; each executes an adaptive refinement feedback loop, but with the adaptive refinement largely restricted to its own subregion. This step is done on all processors with no communication. In this example, each processor adaptively solved a problem with approximately 20K vertices, with a mesh refined in its region and coarse elsewhere.
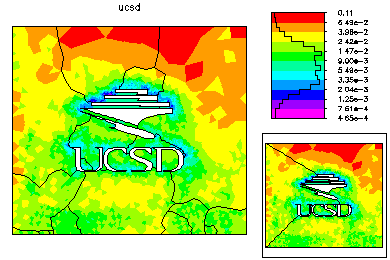
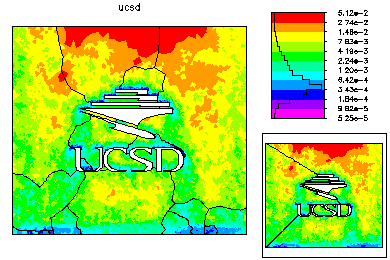
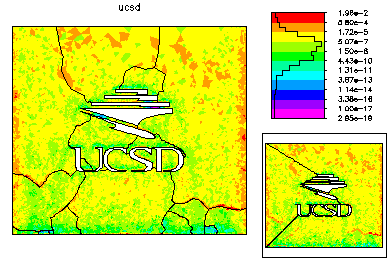
The refined meshes for each processor are then combined to form a global mesh. This mesh is generally nonconforming along the interfaces. The global mesh is made conforming by adjusting the vertices along the interface; the final global mesh has about 224k vertices. A nonconforming solution generated from the fine parts of the solution on each processor is used as initial guess for the final solution on the global mesh. On the left is the global mesh colored by size. On the right is the global mesh colored by element error.
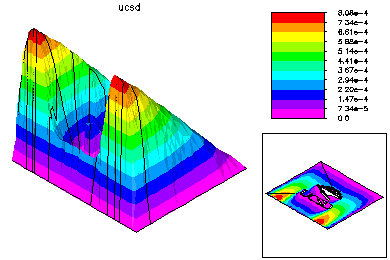
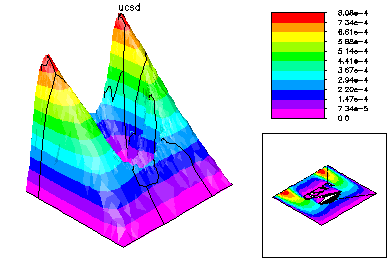
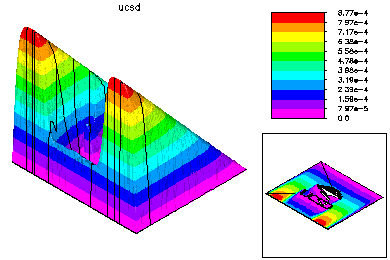
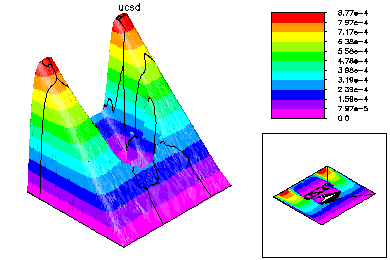
The final global conforming solution is generated by a special domain decomposition algorithm, based on solving global problems on the meshes generated on each processor. This DD solver also has very low communication costs. |