A Nonlinear Eigenvalue Problem
In this problem, we solve the nonlinear eigenvalue problem -Laplace u= \lambda sin(u) on the unit square with Dirichlet boundary conditions. The problem is solved using the continuation options in PLTMG. The continuation is carried out on a uniform coarse mesh.
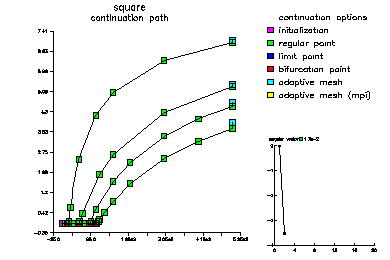
We compute the first four eigenfuctions. Here is a picture of the continuation path. At the points colored cyan the mesh is adaptively refined and a more accurate approximation is computed.
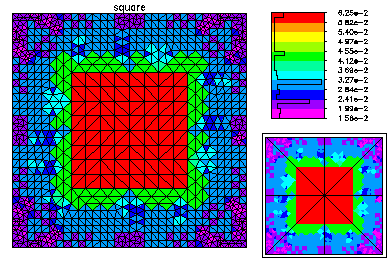
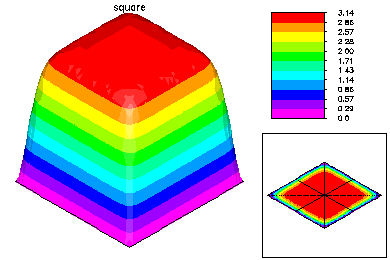
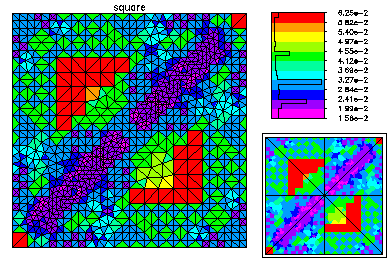
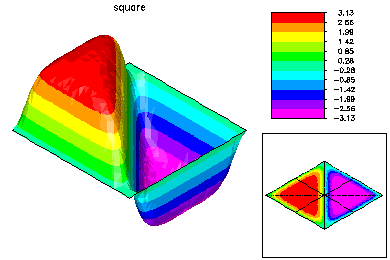
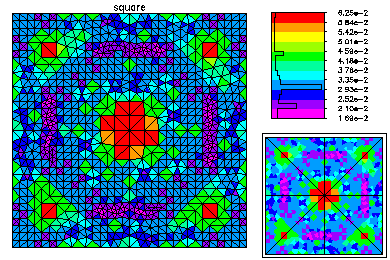
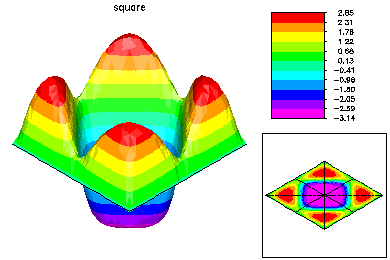
Here is the refined mesh and the first eigenfunction. The refined mesh is colored by element size.
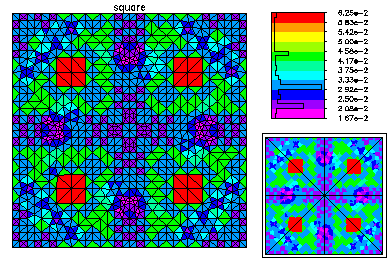
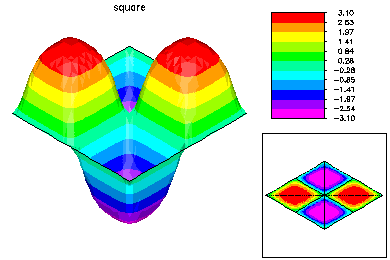
Here is the refined mesh and the second eigenfunction. The second eigenvalue has multiplicity two, but only a single (arbitrary) eigenfuction is computed.
Here is the refined mesh and the third eigenfunction.
Here is the refined mesh and the fourth eigenfunction. The fourth eigenvalue also has multiplicity two. |