A Symmetry-Breaking Bifurcation Problem
In this problem, we solve the nonlinear elliptic problem -0.1 Laplace u + u =\lambda exp(u) on the unit square with homogeneous Neumann boundary conditions. This problem illustrates the continuation options available in PLTMG. The continuation is carried out on a uniform coarse mesh.
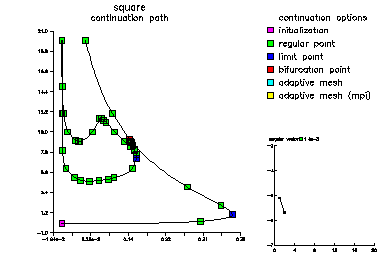
Here is a picture of the continuation path. Points marked blue are limit (turning) points. Those marked red are bifurcation points. All marked points are computed in the continuation process. The solution on the primary branch is constant.
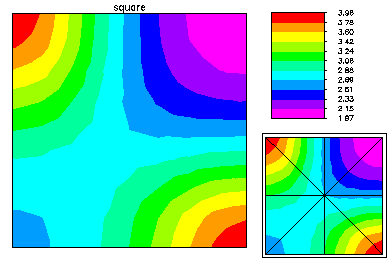
On the secondary branch the solution has less symmetry. The left picture is near the bifurcation point, while the right is near the end of the computed portion of the secondary branch.
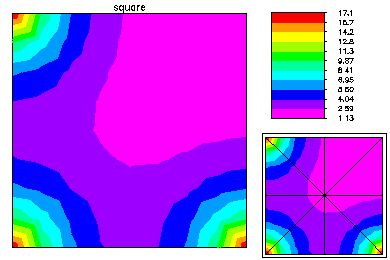
On the tertiary branch the solution has even less symmetry. The left picture is near the bifurcation point, while the right is near the end of the computed portion of the tertiary branch. |