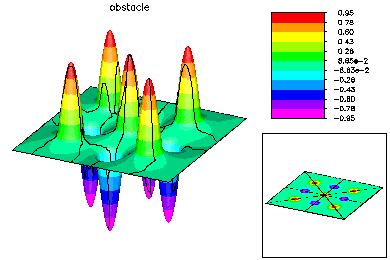
A Minimal Surface Equation with Obstacles

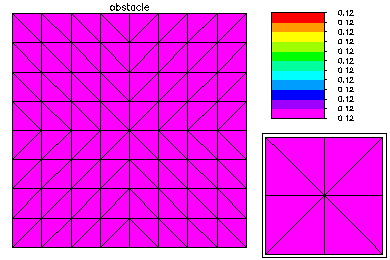
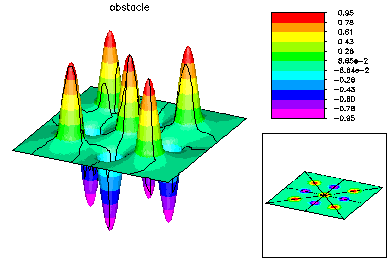
In this example, we solved a minimal surface problem in the unit square, subject to homogeneous Dirichlet boundary conditions and the constraints lwr(x,y) ≤ u(x,y) ≤ upr(x,y). The obstacles were upward and downward facing Gaussian shaped spikes, layed out in a 3 x 3 checkerboard pattern.

This problem was solved using quadratic finite elements. An interior point method was used to handle the constraints. Parallel adaptive meshing using 16 processors was used to create a final global mesh with approximately 50K vertices and 187K degrees of freedom. Above is the initial coarse 9 x 9 mesh and corresponding solution.

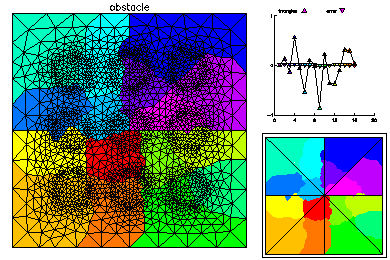
The initial mesh was adaptively refined on one processor to 2k vertices. This mesh was partitioned for 16 processors according to equal error, where the error is estimated via an a posterior error estimator. On the right the load balance is shown without element edges lined with black, and elements are colored according to size.

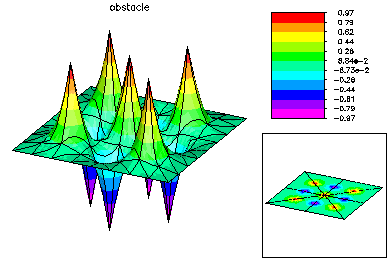
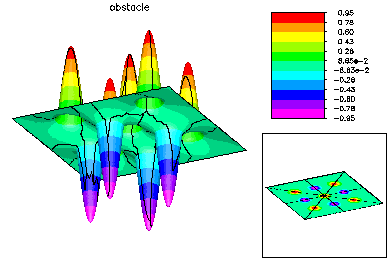
This is the solution on the mesh with 2K vertices.

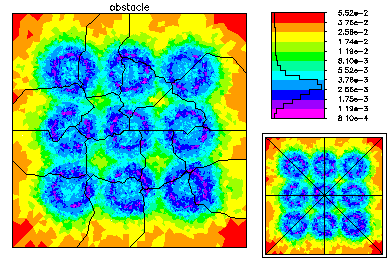
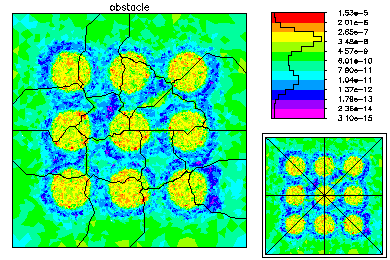
The global mesh has about 50K vertices. On the left is the global mesh colored by size. On the right is the global mesh colored by element error.

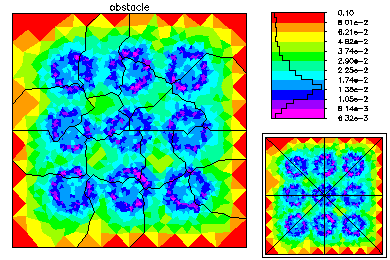
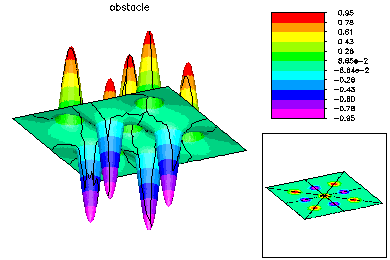
The global mesh has about 187K degrees of freedom. Here are some pictures of the fine global fine grid solution.