The Multilevel Multigraph Iterative Method

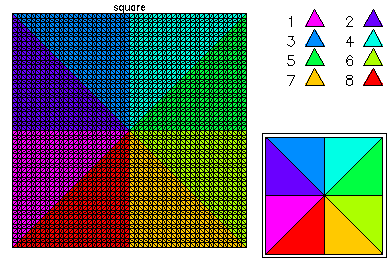
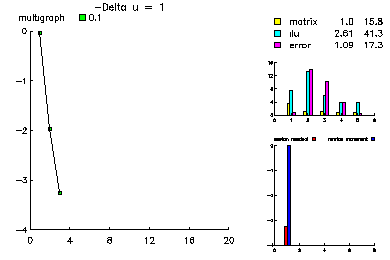
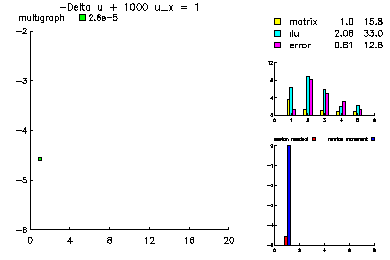
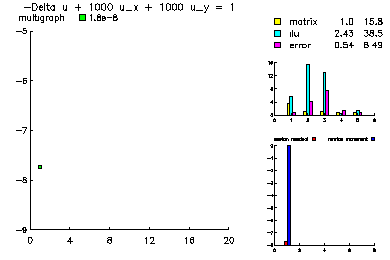
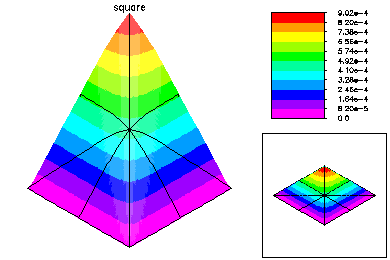
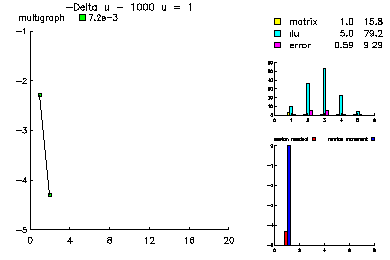
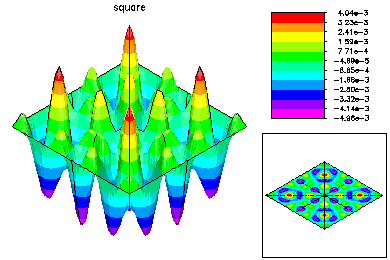
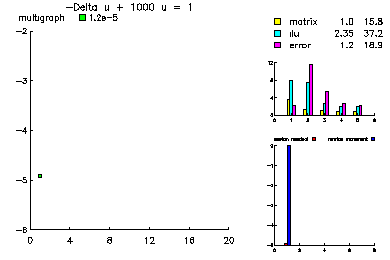
In this example, we show the convergence history of the multilevel-multigraph iterative method on a selection of simple partial differential equations. All are solved on the this 101 x 101 uniform triangulation of the unit square. All problems have homogeneous Dirichlet boundary conditions. The multilevel multigraph iterative method based on principles of classical multigrid methods. However, it is completely algebraic in nature. The smoother is an ILU using minimum degree ordering and a drop tolerance (in this case 1.e-2). The coarsening procedure is based on the ILU factorization in order to reduce the setup overhead.

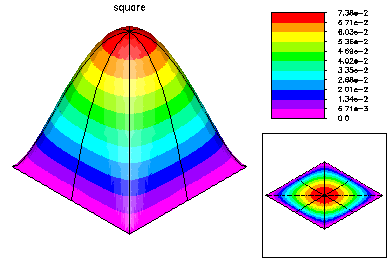
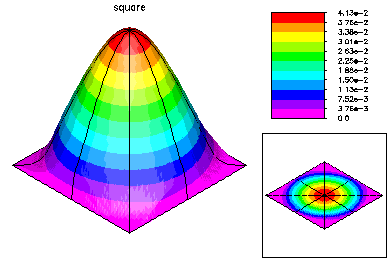
This problem was -Laplace u = 1.

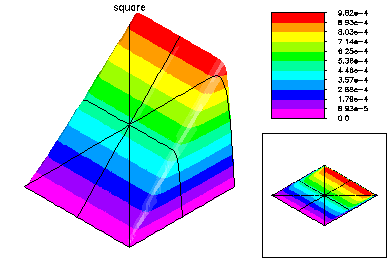
This problem was -Laplace u +1000 u_x = 1.

This problem was -Laplace u + 1000 u_x + 1000 u_y =1.

This problem was -Laplace u - 1000 u = 1.

This problem was -Laplace u + 1000 u = 1.

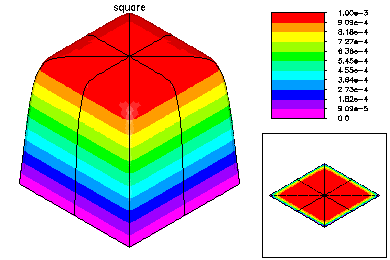
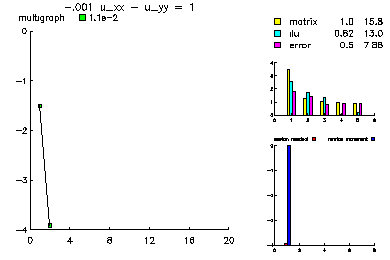
This problem was -.001 u_xx - u_yy = 1.

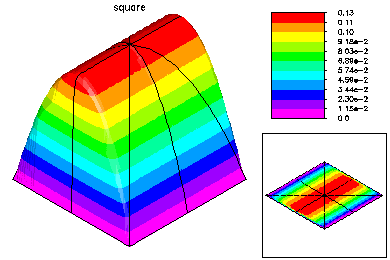
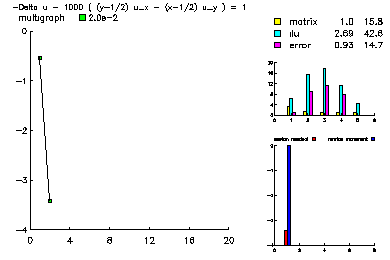
This problem was -Laplace u + 1000 ( u_x (y-.5) - u_y (x-.5) ) = 1.